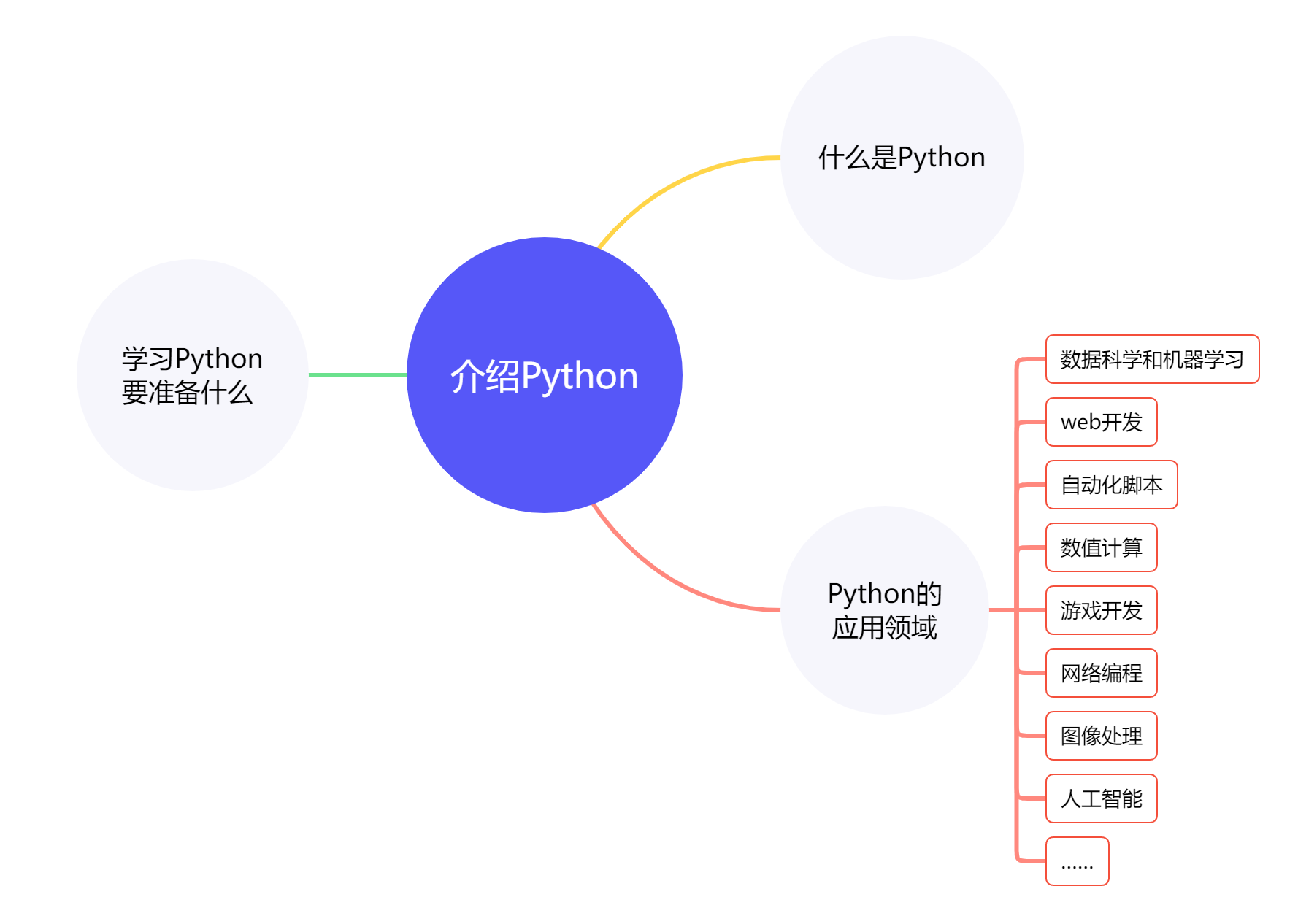
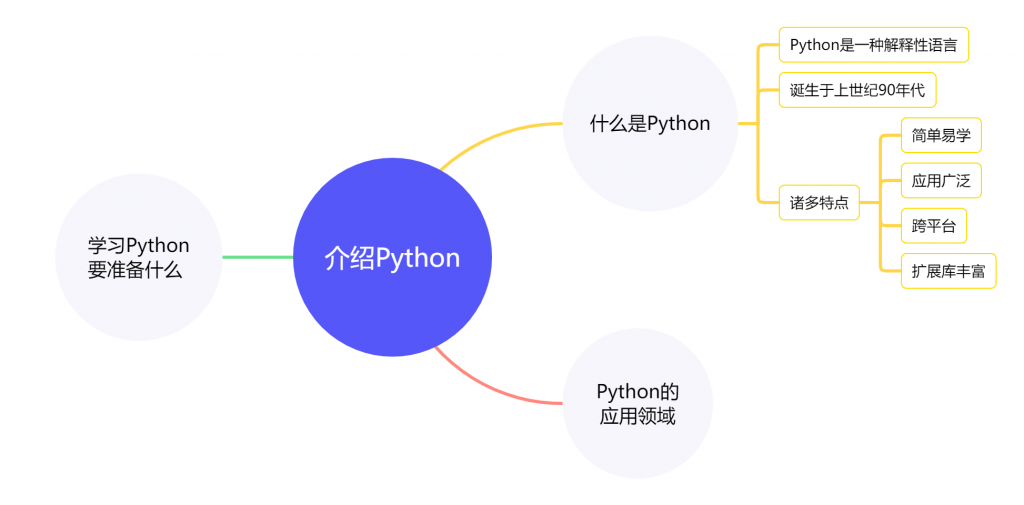
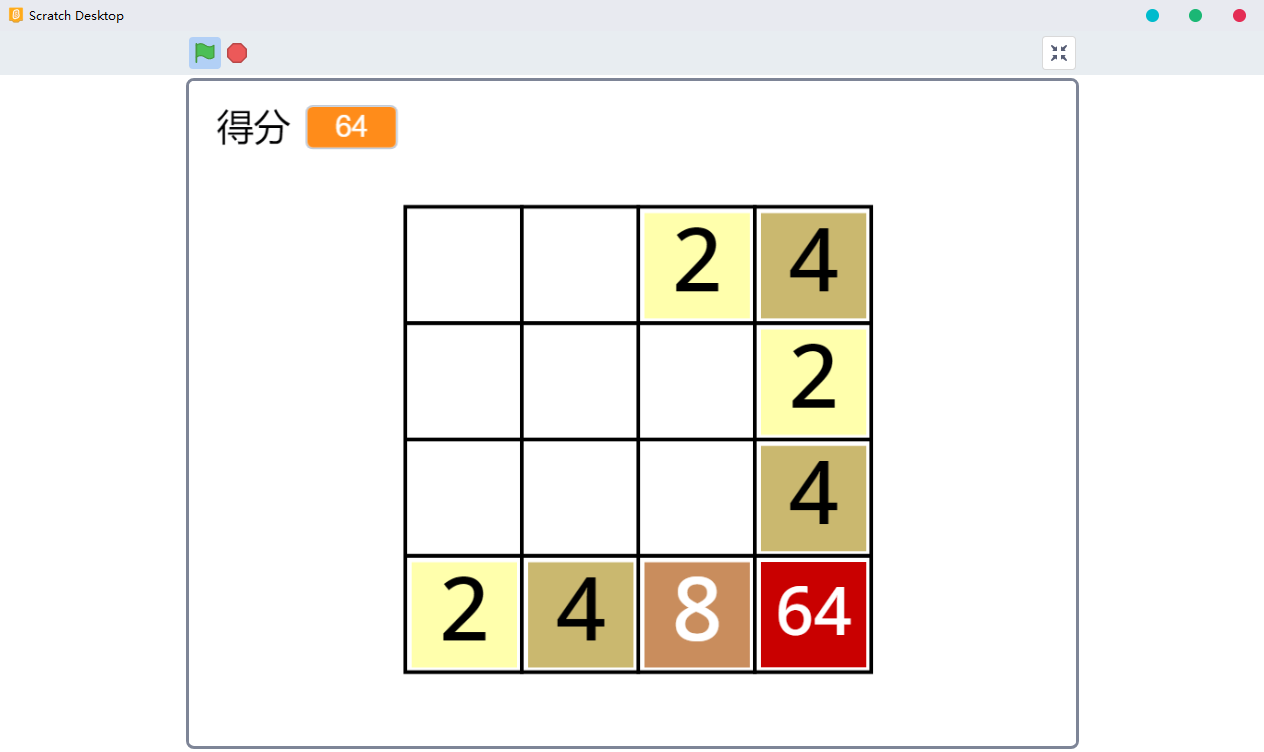
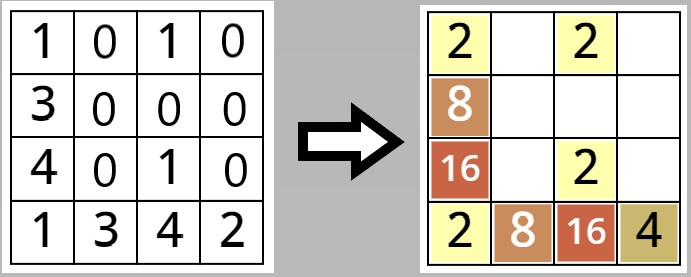
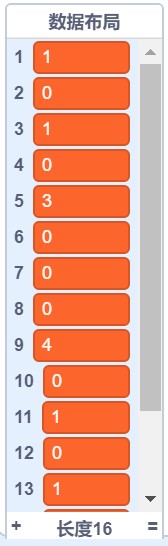
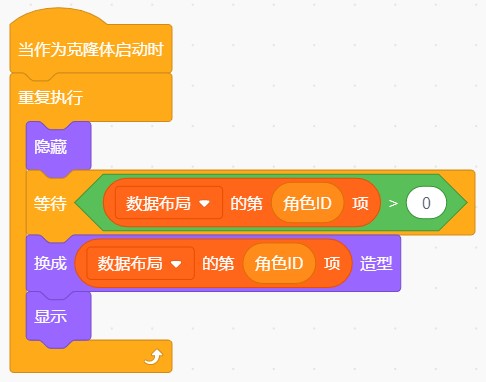
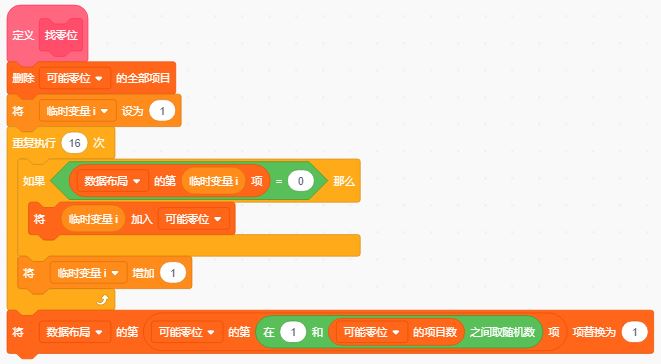
上节课最后,我们把制作右移操作积木块的任务当成了作业布置下去,大家做的如何呢?下面我们先简单看一下老师这边的实现情况。
我们再稍微往细致思考一下,还记得上节课分析出来的三个步骤吗?
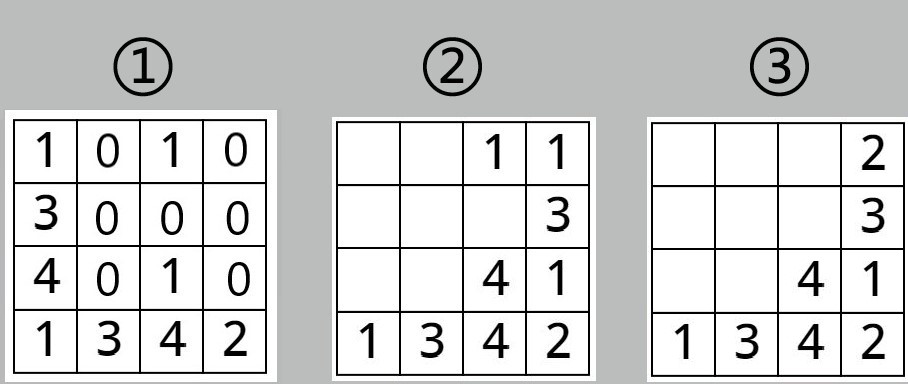
第①个,删除同行的所有“0”。在下面~
我们第①步要做的是删除每行所有的“0”,那么我们自然不能在【数据布局】这个大的列表中进行删除,因为这样会影响到这个列表的排列顺序,所以我们选择一个比较稳妥的方法,将每行的元素取出到一个临时列表变量【待处理元素】中,每次放一行共4个元素,然后我们开始在这个小的列表里进行处理。
既然要放到这个小列表里,那么我们首先要保证这个小列表里是空的,即便它本来是空的,我们也应该在开始时进行一个初始化,删除掉它当中的所有元素。然后我们就可以依次放入第一行的内容了,用我们刚才得出的公式,嵌入到一个4次循环中,每次取出一个,放入到【待处理元素】中。我们发现这个公式里要考虑两个变量——行号和列号,所以我们需要两个临时的变量来用于计算。
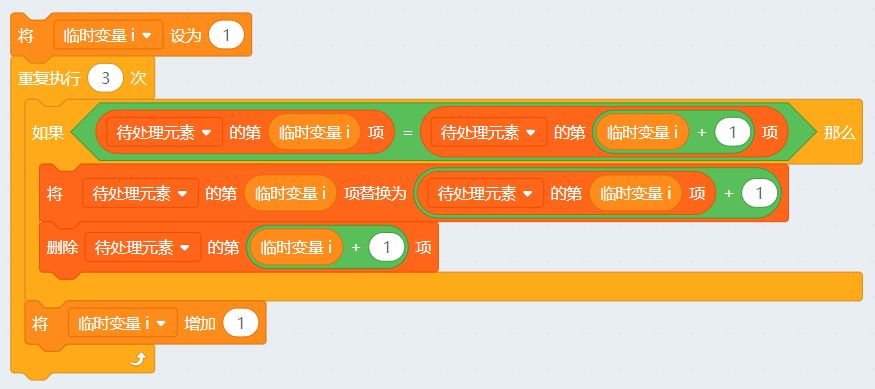
这里要注意添加到小列表时的顺序 对应行的内容我们取到了,“0”我们也去掉了。
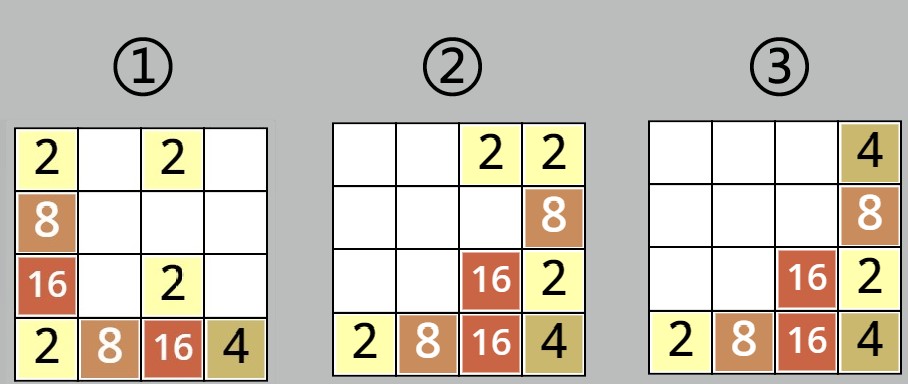
使用一个临时变量,完成了一行的4个元素的比较 好了,下面剩下最后一步了,第③步,补“0”使得该行总数为4。
为了完成这最后一步的要求,我们要先把【待处理元素】这个列表中补齐4个元素,这个简单。
用0补齐 最后,我们按照顺序,用【待处理元素】列表中的元素,替换【数据布局】里对应行的元素,之后就完成咯。
这部分内容留给大家做本次内容的作业吧!